First-Principles Phonon Quasiparticle Theory Applied to a Strongly Anharmonic Halide Perovskite

Abstract

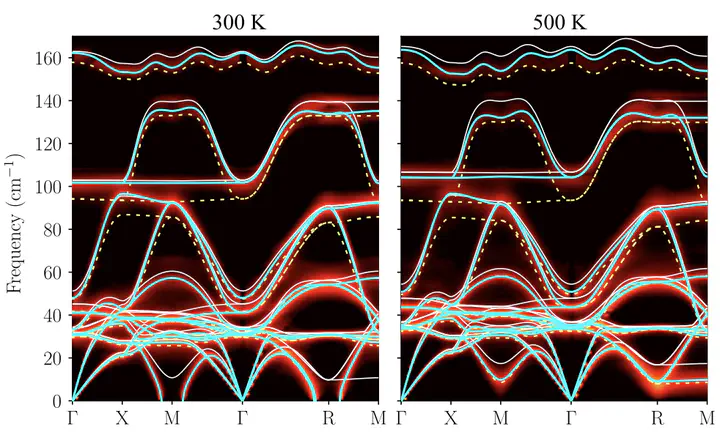
Understanding and predicting lattice dynamics in strongly anharmonic crystals is one of the long-standing challenges in condensed matter physics. Here, we propose a first-principles method that gives accurate quasiparticle (QP) peaks of the phonon spectrum with strong anharmonic broadening. On top of the conventional first-order self-consistent phonon (SC1) dynamical matrix, the proposed method incorporates frequency renormalization effects by the bubble self-energy within the QP approximation. We apply the developed methodology to the strongly anharmonic $α$-CsPbBr_3 that displays phonon instability within the harmonic approximation in the whole Brillouin zone. While the SC1 theory significantly underestimates the cubic-to-tetragonal phase transition temperature ($T_c$) by more than 50%, we show that our approach yields $T_c=$404-423 K, in excellent agreement with the experimental value of 403 K. We also demonstrate that an accurate determination of QP peaks is paramount for quantitative prediction and elucidation of the phonon linewidth.

Terumasa Tadano

Researcher of Materials Science

My research interests include development of computational methods and softwares for predicting thermal properties of solids, and application of machine-learning methods to material science study